exponentiell mit n, gn
(Goldener Schnitt; g2 = g + 1; g = 1,618...)
Iterative Form der Berechnung der Fibonacci-Zahlen:
Idee: Zwei ganze Zahlen a und b werden mit 0 und 1 initialisiert und wie folgt hochgezählt:
- a := a+b,
- b := a.
public int fib (int n) {
return fib_iter (1,0,n);
}
private int fib_iter (int a, int b, int zaehler) {
if (zaehler == 0) return b;
else return fib_iter ((a + b), a, --zaehler);
}
(defun fib (n)
(fib-iter 1 0 n))
(defun fib-iter (a b zaehler)
(if (= zaehler 0) b
(fib-iter (+ a b) a (1- zaehler))))
Kombinatorisches Problem: Berechnung des Wechselgelds
komplizierteres Beispiel:
Wieviele Möglichkeiten gibt es, 1,- DM zu wechseln
(in 50, 10, 5, 2, 1-Pfennig-Münzen)?
# Betrag a mit n Münzen wechseln =
# Betrag a mit (n-1) Münzen wechseln +
# Betrag (a-d) mit n Münzen wechseln, wobei d = Wert der ersten Münze
- a = 0 -> 1 Wechselmöglichkeit
- a < 0 -> 0 Wechselmöglichkeiten
- n = 0 -> 0 Wechselmöglichkeiten
in Java:
int wg (int betrag, int muenzarten) {
if (betrag == 0) return 1;
else if ((betrag < 0) || (muenzarten == 0)) return 0;
else return
wg (betrag, --muenzarten) +
wg ((betrag - erster_nennwert (muenzarten)), muenzarten);
}
int erster_nennwert (int m) {
if (m == 1) return 1;
else if (m == 2) return 2;
else if (m == 3) return 5;
else if (m == 4) return 10;
else return 50;
}
(defun wg (betrag muenzarten)
(cond ((= betrag 0) 1)
((or (< betrag 0) (= muenzarten 0)) 0)
(t (+ (wg (- betrag (erster-nennwert muenzarten)) muenzarten)
(wg betrag (- muenzarten 1))))))
(defun erster-nennwert (muenzarten)
(case muenzarten (1 1) (2 2) (3 5) (4 10) (5 50)))
Aufruf: wg (100, 5) -> 2498.
2.4 Komplexität rekursiver Verfahren
N=10 N=20 N=100 N=106 O(1) 1 1 1 1 O(log n) 3.32 4 6 19.9 O(n) 10 20 100 106 O(n log n) 33.2 80 600 1.99*107 O(n2) 100 400 10 000 1012 O(2n) 1 000 1 000 000 1 000 000 000 000 000 000 000 000 000 000 10300 000
Rechenzeit Speicherplatz Fakultät rekursive Version O(n) O(n) iterative Version O(n) O(1) Fibonacci baumrekursive Version O(gn) O(n) iterative Version O(n) O(1)
Potenzrechnung
in Java:
public int potenz1 (int b, int n) {
if (n == 0) return 1:
else return b * potenz1 (b, --n);
}
public int potenz2 (int b, int n) {
return pot_iter (b, n, 1);
}
private int pot_iter (int b, int zaehler, int produkt) {
if (zaehler == 0) return produkt;
else return pot_iter (b, (zaehler-1), (b * produkt));
}
public int potenz3 (int b, int n) {
if (n == 0) return 1;
else if (isGerade(n)) return quadrat (potenz3 (b, (n / 2)));
else return b * potenz3 (b, (n-1));
}
boolean isGerade (int a) {
return ((n % 2) == 0);
}
int quadrat (int a) {
return a*a;
}
in Lisp:
(defun potenz1 (b n)
(if (= n 0) 1
(* b (potenz1 b (1- n)))))
(defun potenz2 (b n)
(pot-iter b n 1))
(defun pot-iter (b zaehler produkt)
(if (= zaehler 0) produkt
(pot-iter b (1- zaehler) (* b produkt))))
(defun potenz3 (b n)
(cond ((= n 0) 1)
((evenp n) (quadrat (potenz3 b (/ n 2))))
(t (* b (potenz3 b (1- n))))))
Rechenzeit Speicherplatz Potenzen rekursive Version O(n) O(n) iterative Version O(n) O(1) effiziente rek. Version O(log n) O(log n) effiziente iter. Version O(log n) O(1)
2.5 Abstraktionen mit Funktionen höherer Ordnung
Mächtiges Abstraktionsprinzip: Funktionen, die Funktionen als
Argumente haben.
Berechnung von Summen
in Java:
weil: 1/(1*3) + 1/(5*7) + 1/(9*11) + ... gegen p/8
konvergiert allgemein: in mathematischer Schreibweise: b å f(n) = f(a) + ... + f(b) n=a, step x
Gesucht x, so daß f(x) = 0.
in Java:
int einfachsumme (int a, int b) {
if (a > b) return 0;
else return a + einfachsumme (++a, b);
}
int kubiksumme (int a, int b) {
if (a > b) return 0;
else return a*a*a + kubiksumme (++a, b);
}
double pisumme (int a, int b) {
if (a > b) return 0;
else return 1/(a*(a+2)) + pisumme((a+4), b);
}
in Lisp:
(defun einfachsumme (a b)
(if (< a b) 0
(+ a (einfachsumme (+ a 1) b))))
(defun kubiksumme (a b)
(if (< a b) 0
(+ (* a a a) (kubiksumme (+ a 1) b))))
(defun pisumme (a b)
(if (< a b) 0
(+ (/ 1 (* a (+ a 2)) (pisumme (+ a 4) b))))
double <name> (double a, double b) {
if (a > b) return 0;
else return (<funktion> a) + <name> (<naechster> a), b);
}
(defun <name> (a b)
(if (< a b) 0
(+ (<funktion> a) (<name> (<nächster> a) b))))
in Java:
interface UnaryFunction {
public double execute (double a);
}
double summe (UnaryFunction f, double a, UnaryFunction naechstes, double b) {
if (a > b) return 0;
else return f.execute (a) + summe (f, naechstes.execute (a), naechstes, b);
}
double kubiksumme (double a, double b) {
return summe (
new UnaryFunction () {
public double execute (double x) { return x*x*x; } },
a,
new UnaryFunction () {
public double execute (double x) { return x+1; } },
b );
}
// der Aufruf "kubiksumme (1, 5)" liefert 225
double pisumme (double a, double b) {
return summe (
new UnaryFunction () {
public double execute (double x) {
return 1/(x*(x+2)); } },
a,
new UnaryFunction () {
public double execute (double a) {
return a+4; } },
b );
}
in Lisp:
(defun summe (f a naechstes b)
(if (> a b) 0
(+ (funcall f a) (summe f (funcall naechstes a) naechstes b))))
Berechnung des Integrals einer Funktion f
in Java:
![]() ~ [ f(a + dx/2) + f (a + dx + dx/2) + ... + f(b - dx/2) ] * dx,
wobei dx = (b-a)/n.
~ [ f(a + dx/2) + f (a + dx + dx/2) + ... + f(b - dx/2) ] * dx,
wobei dx = (b-a)/n.
double integral (UnaryFunction f, double a, double b, double dx) {
return dx * summe (f, (a + dx/2),
new UnaryFunction () {
public double execute (double a) {
return a + dx;
} },
(b - dx/2));
}
// Aufruf:
integral (new UnaryFunction () {
public double execute (double a) {
return a*a*a;
} }, 0, 1, 0.01)
in Lisp:
(defun integral (f a b dx)
(* (summe1 f (+ a (/ dx 2)) 'add-dx b) dx))
(defun add-dx (x dx)
(+ x dx))
;;; Aufruf:
(defun kubik (x) (* x x x))
(integral `kubik 0 1 0,01) -> 0,249987
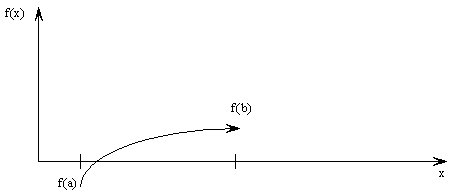
Berechnung der Nullstellen einer Funktion mit der Methode der
Intervallhalbierung
Voraussetzung: f(a) < 0 < f(b)
Technik für Nullstellenberechnung "NSB" (a, b):
double nullSuche (UnaryFunction fun, double neg, double pos) {
final double mittelpunkt = ((neg + pos) / 2);
final double testWert = fun.execute(mittelpunkt);
if (nahGenug(pos, neg)) return mittelpunkt;
else if (testWert > 0) return nullSuche(fun, neg, mittelpunkt);
else if (testWert < 0) return nullSuche(fun, mittelpunkt, pos);
else return mittelpunkt;
}
double intervallHalbierung (UnaryFunction fun, double a, double b) {
final double aWert = fun.execute(a);
final double bWert = fun.execute(b);
if (nahGenug(aWert, 0)) return a;
else if (nahGenug(bWert, 0)) return b;
else if ((aWert < 0) && (bWert > 0)) return nullSuche(fun, a, b);
else if ((aWert > 0) && (bWert < 0)) return nullSuche(fun, b, a);
else {
System.out.println("Eingabewerte haben gleiches Vorzeichen.");
return 0.0;
}
}
boolean nahGenug (double x, double y) {
return (Math.abs (x-y) < 0.001);
}
// Aufruf: liefert 3.1411132
intervallHalbierung (
new UnaryFunction() {
public double execute (double a) {
return (double) Math.sin(a); } },
2, 4);
in Lisp:
(defun null-suche (f neg-punkt pos-punkt)
(labels ((nah-genug? (x y) (< (abs (- x y)) 0.001)))
(let* ((mittelpunkt (/ (+ neg-punkt pos-punkt) 2))
(test-wert (funcall f mittelpunkt)))
(cond ((nah-genug? neg-punkt pos-punkt) mittelpunkt)
((plusp test-wert) (null-suche f neg-punkt mittelpunkt))
((minusp test-wert) (null-suche f mittelpunkt pos-punkt))
(t mittelpunkt) ;;; dieser Fall darf eigentlich nicht vorkommen!
))))
(defun intervall-halbierung (f a b) ;;; testet Voraussetzungen fuer null-suche
(let ((a-wert (funcall f a))
(b-wert (funcall f b)))
(cond ((zerop a-wert) a)
((zerop b-wert) b)
((and (minusp a-wert) (plusp b-wert)) (null-suche f a b))
((and (minusp b-wert) (plusp a-wert)) (null-suche f b a))
(t (print "Eingabewerte haben gleiches Vorzeichen")))))
;;; Aufruf: (intervall-halbierung 'sin 2.0 4) liefert 3.14111328125
Berechnung des Skalarprodukts in Prolog:
inner_product([X|Xs], [Y|Ys], Z) :-
inner_product(Xs, Ys, U),
Z is U + X*Y.
inner_product([], [], 0).
Berechnung des Skalarprodukts mit maplist in Prolog:
inner_product(Xs, Ys, Z) :-
pair_lists(Xs, Ys, Ps),
maplist( multiply,
Ps, Zs ),
add(Zs, Z).
multiply([X,Y], Z) :-
Z is X * Y.
% Bibliothekspraedikate
% - pair_lists/3
% - add/2
pair_lists([X|Xs], [Y|Ys], [[X,Y]|Zs]) :-
pair_lists(Xs, Ys, Zs).
pair_lists([], [], []).
add([X|Xs], Y) :-
add(Xs, Z),
Y is X + Z.
Diese Implementierung ist zwar etwas umfangreicher als ohne maplist,
aber sie ist übersichtlicher,
falls die Bibliotheksprädikate schon zur Verfügung stehen.
2.6 Prozeduren als Ergebnis
Prozeduren erzeugen Prozeduren:
z.B.: die Ableitung von x3
ist 3x2.
Die Ableitung ist selbst wieder eine Prozedur,
die auf Argumente angewandt werden kann.
unaryFunction ableitung (unaryFunction f, double dx) {
return
new unaryFunction () {
public double execute (double x) {
return (f.execute (x + dx) – f.execute (x)) / dx; } };
}
// Aufruf: Ableitung der Quadrat-Funktion an der Stelle 5
ableitung (
new unaryFunction () {
public double execute (double a) {
return a*a; } },
0.001).execute (5);
in Lisp:
(defun ableitung (f dx)
#'(lambda (x)
(/ (- (funcall f (+ x dx))
(funcall f x))
dx)))
;;; Aufruf: Ableitung der Funktion "kubik" an der Stelle 5
(defun kubik (x) (* x x x)) ;;; Wdh
;;; (ableitung 'kubik .001) -> #<Compiled-Lexical-Closure #xE283B6>
;;; (funcall (ableitung 'kubik .001) 5) -> 75.01500100002545
Vorteil von Prozeduren als Ergebnis:
Man kann nicht nur mit vorbestimmten Prozeduren Berechnungen durchführen,
sondern auch mit solchen, die sich aus der laufenden Berechnung ergeben.